
Shortly after it occurred, scientists said there was a slight chance Monday’s magnitude-4.4 earthquake in Los Angeles may have been a “foreshock” of a bigger one yet to come. That’s obviously getting less likely by the day, but still: Let’s say an impressive-looking seismologist gets on TV and says there’s going to be a magnitude 7.0 quake tomorrow. “Whoa,” you’d likely say to yourself. “That sounds pretty big.” Imagine she then got back on TV and revised her estimate: Actually, it’s going to be magnitude 7.2 quake. “Was that really worth another announcement?” you’d likely ask. “I’m trying to watch Scandal here.”
And that is why the common way of measuring earthquakes is so unhelpful for you, me, and everyone else who doesn’t understand the finer points of seismology. As it turns out, a magnitude-7.2 earthquake is twice as strong as a magnitude-7.0 earthquake in terms of the amount of energy released. The common scale we use to measure earthquakes is actually almost entirely useless as a way of communicating the power of earthquakes to anyone but mathematicians and seismologists — it confuses more than it informs. It’s a maddeningly unclear system.
Without getting into the math-y particulars, there’s an important distinction between a logarithmic scale, which is how scientists measure earthquakes, and the so-called linear scales we deal with in everyday life: On a linear scale, we know that four is twice as big as two and eight twice as big as four. This is what a casual observer of earthquake magnitude scales would expect: that an earthquake of 6.0 packs twice the punch of a 3.0. But no! In reality, a 6.0 quake releases 31,622.776 times as much energy as a 3.0 quake. And a 7.0 releases 31.622 times as much energy as a 6.0.
That’s because logarithmic scales, which are how scientists measure earthquakes (there are multiple different scales currently in use, but they all give approximately the same results for the same earthquakes), work differently. Here, each item you move down the number line (from 1 to 2 to 3 to 4 … ) corresponds not with a simple one-unit increase, but with an order of magnitude increase. So, to slightly oversimplify things, a magnitude-3.0 quake displaces the Earth ten times as much as a magnitude-2.0 quake, which in turn displaces the Earth ten times as much as a magntiude-1.0 quake (and these all translate into different amounts of energy released).
If you’re at all like me, mere mention of the term “order of magnitude” will induce eye-glazing, and that’s because it runs contrary to our usual understanding of numbers, in which the difference between 19 and 20 is the same as the difference between 20 and 21 (a difference of one, for those without access to a calculator).
But when we’re measuring earthquakes, the difference between two numbers in terms of raw energy released gets bigger and bigger the further up the scale we go. So a 1.2 quake is a little bigger than a 1.0 quake, but a 7.2 quake is much bigger than a 7.0 quake. Since we’re used to linear scales, this means that the intuitive way most people understand the earthquake scales — say, that anything below 3 is small, 3 to 6 is medium, and 6 or higher is big — is way off. When you get to really high numbers, the amounts of energy are in an entirely different ballpark, so the difference between a 7.0 quake and a 6.0 quake is, in terms of energy released, itself equivalent to about 722 magnitude-5.0 quakes (according to numbers I stole from here). So if you assume that a 7.0 is just a bit bigger than a 6.0 — which would be totally understandable, given that that’s how numbers work in just about every facet of our lives — you may find yourself in trouble.
Here, via the government, is a good example of how all this stuff works in practice when it comes to the retired Richter scale:
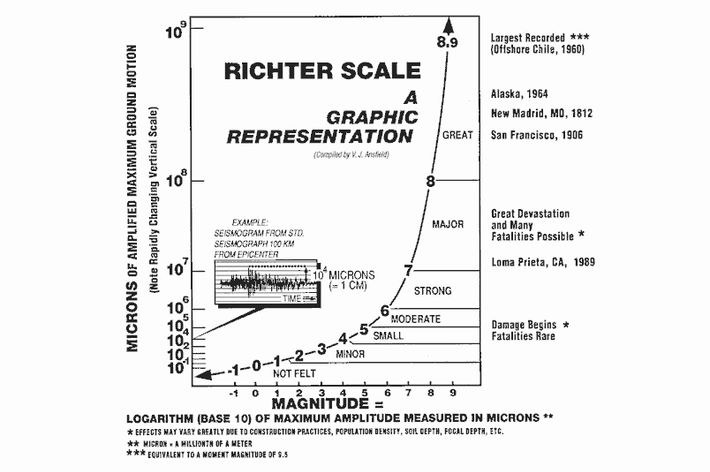
Now, there’s a perfectly good reason for some people to use a logarithmic scale — it’s a useful way for scientists to deal with measuring a phenomenon, like an earthquake, in which a large instance of said phenomena is much, much, much bigger than a small instance of said phenomena, because otherwise things get a bit numerically messy. (As is so often the case with anything nerdy or math-y, xkcd covers this nicely. There’s a more comprehensive, slightly technical explanation here.)
But from a public-safety perspective, logarithmic scales aren’t just confusing, they’re dangerous. While magnitude scales are obviously used by scientists for a variety of reasons — not least comparing different quakes that occur at different times in history — an ideal measurement system for public consumption would be one that the average person sitting in an earthquake-prone area could quickly understand and translate into the appropriate reaction, whether “Meh,” “I must make peace with my god(s),” or something in between. The logarithmic scale is not compatible with this sort of intuitive simplicity.
Unfortunately, a linear scale isn’t a perfect alternative, either. If you rescaled things to a linear scale — such as how much energy is produced by a given quake — suddenly you’d be dealing with huge numbers for the big quakes. And huge numbers are another thing most people aren’t particularly good at grasping.
What it comes down to is that earthquakes, unlike windspeed, temperature, or other day-to-day numbers reported in the news, are not straightforward things to measure. They originate in one place and radiate outward and are felt differently everywhere else. Total energy is not the same as the amount of Earth displaced, and so on. So this sort of measurement might befuddle people, but we’re probably simply stuck with it for now. Meaning those living out west might want to catch up on their logarithmic scales.





























